Was ist eigentlich Mathematik in der Grundschule?

Kinder im Vor- und Grundschulalter haben oft ein unbefangenes Verhältnis zur Mathematik. Zählen, Vergleichen, Ordnen sind Tätigkeiten, die mit viel kreativem Spaß und oftmals direkten Erfolgserlebnissen verbunden sind. Für Kinder hat Mathematik dabei oft eine fast magische Komponente: „Alles geht so schön auf“ oder „Die Dinge passen überraschend gut zueinander“.

Mit einer solchen Herangehensweise sind Kinder in diesem Alter dem Bild, das ein „richtiger Profimathematiker“ von Mathematik hat, oftmals auf überraschende Weise näher, als zu vielen späteren Zeitpunkten ihrer Schullaufbahn.

Denn für das Mathematik-Lernen sind drei Grunderfahrungen notwendig:

1. Erscheinungen unserer Welt können wir erkennen und durch mathematische Berechnung besser verstehen.

2. Wir können mathematische Gegenstände und Sachverhalte als eine geordnete Welt eigener Art wahrnehmen und verstehen.

3. Wir müssen Problemlösefähigkeiten erwerben, die über die Mathematik hinausgehen!

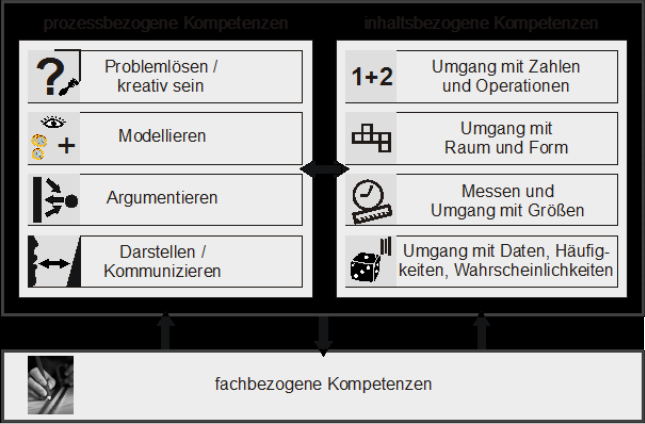
siehe Lehrplan Mathematik

https://www.schulentwicklung.nrw.de/lehrplaene/lehrplannavigator-grundschule/mathematik/lehrplan-mathematik/bereiche/bereiche.html

Aber wie kommen die Zahlen und Operationen in den Kopf?

Wenn es um Festigung von Zahlbegriffen geht, so ist die Orientierung am Zehnersystem maßgeblich. Das Zehnersystem liegt dem Menschen körperlich nahe (zehn Finger, zehn Zehen) und ist aufs engste mit der Sprache verknüpft. Fundamental für alles Weitere ist somit die Bildung der Zahlbegriffe von 1 bis 10.

Diese Begriffe sind dann gefestigt, wenn das Kind eine entsprechende Anzahl, die vor seinen Augen liegt, auf einen Schlag (ohne zu zählen) identifizieren kann, und zwar völlig fehlerfrei. Solange dies nicht geht, ist jede operative Verknüpfung von Zahlen (Addition, Subtraktion usf.) ohne Fundament.

Es ist für den gesamten Mathematikunterricht auch von größter Bedeutsamkeit, dass die Kinder in den ersten Wochen des ersten Schuljahrs durch systematische Übungen lernen, Anzahlen statt durch Elemente weises Zählen durch eine Strukturierung der Menge in übersichtliche und leicht addierbare Teilmengen zu ermitteln. Der Mensch kann in der Regel nur 4 Elemente auf einen Schlag in jeder beliebigen Anordnung identifizieren und deshalb sollte die Vorgabe von 5 oder mehr Elementen immer gesetzmäßig strukturiert sein muss. Dabei ist wichtig, dass das Kinder die jeweilige Zahl nicht nur in einer optischen Gestalt (z.B. die Fünf des Würfelbildes) erkennt, sondern in jeder möglichen Kombination.

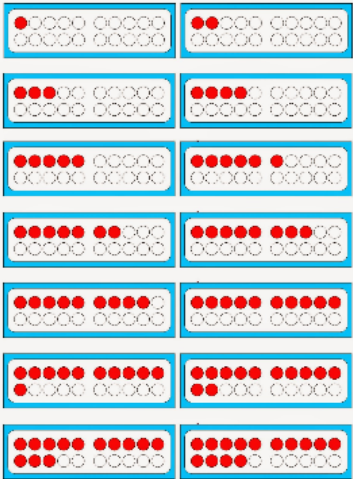
Dazu dienen als Veranschaulichungsmittel strukturierte Materialien (Cuisenaire Stäbe, Zwanziger Feld, Rechenschiffe, Rechenrahmen, Rechenkette, Zahlenstrahl), die als zentrale Hilfsmittel den Kindern bei der Entwicklung und Festigung des Zahlverständnisses und beim Rechnen helfen sollen.

Voraussetzungen für das Mathematiklernen sind konkrete Handlunge, denn besonders Handlungen mit Material erzeugen Vorstellungsbilder!

Jede arithmetische Tätigkeit ist sinnlos, wenn sie nicht auf gefestigten Zahlbegriffen beruht. Erst- und Zweitklässler zeigen es dem Lehrer sehr deutlich, wenn sie noch nicht über gefestigte Zahlbegriff verfügen: Sie zählen weiter (z.B. die Finger, die Äpfel, womit gerechnet wird).

Kinder, die in irgendeiner Klasse im Rechnen versagen, verfügen zumeist nicht über gefestigte Zahlbegriffe. Wenn sie z.B. 100 hören, "sehen" sie innerlich die drei Ziffern, statt eine Anzahl von Elementen, die sich z.B. als zehnmal fünf plus zehnmal fünf oder zehn mal zehn oder das Doppelte von fünfzig strukturieren lässt.

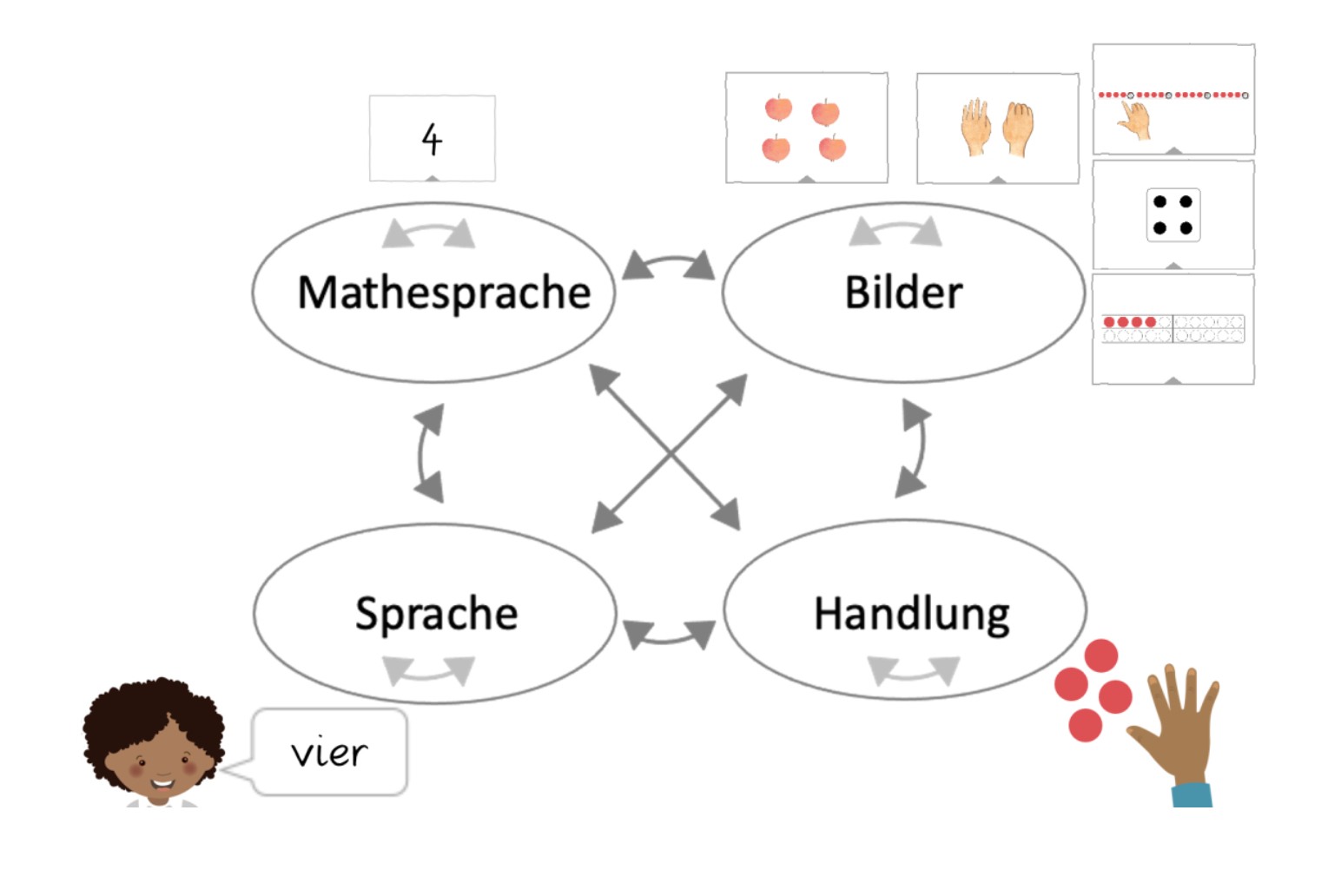
Beim Umgang mit allen Materialien ist das Reflektieren der Vorgehensweise wichtig.

• Wie bist du vorgegangen?

• Was war schwierig an der Aufgabe?

• Wo kamst du noch nicht weiter?

• Was hat dir geholfen?

• Gab es einen Trick?

Diese unterrichtlichen Voraussetzungen werden dazu geschaffen:

• Vereinen von unterschiedliche Lernniveaus

• Lernen in Kleingruppen

• gegenseitiges Erklären und Helfen

• Zulassen von Fehlern und alternativen Lösungen

Lerninhalte chronologisch nach dem Zahlenbuch aufgelistet